True/False
Indicate whether the sentence or statement is true
or false.
|
|
|
For
questions 1 to 6, consider a ball of mass m, thrown at an angle above the horizontal and
undergoing projectile motion under negligible air resistance.
|
|
| 1. | The time for the ball to rise equals the time for the ball to fall to
the same horizontal level.
|
|
| 2. | The net force on the ball at the top of its flight is
zero.
|
|
| 3. | The
acceleration of the ball on the way up equals the acceleration on the way down.
|
|
| 4. | After
leaving your hand and before landing, the speed of the ball is at a minimum at the top of its
trajectory.
|
|
| 5. | The magnitude of the horizontal component of the
velocity of the ball just before impact exceeds the magnitude of the horizontal component of the
velocity just after the ball leaves your hand.
|
|
| 6. | The
magnitude of the acceleration of the ball at the top of its trajectory equals the ratio of the weight
of the ball to its mass.
|
|
|
or questions 7 to 12, assume that you are twirling a small rubber
stopper of mass m (at a constant speed v) tied to a string in a vertical circle as
shown in Figure 1.
Figure
1
For questions 7 to 12
|
|
| 7. | At
position 3, the direction of the instantaneous acceleration is westward and the direction of the
instantaneous velocity is upward.
|
|
| 8. | The
vector quantity  is closest to the instantaneous acceleration as the
stopper moves from position 6 to position 1. is closest to the instantaneous acceleration as the
stopper moves from position 6 to position 1.
|
|
| 9. | The
magnitude of the tension in the string at position 1 exceeds the magnitude of the tension at position
4 by an amount equal to mg.
|
|
| 10. | At position
5, the force that causes the stopper to accelerate toward the centre of the circle is the sum of the
force of tension in the string and a component of the force of gravity on the stopper.
|
|
| 11. | If
you release the ball at the instant it reaches position 1, the instantaneous velocity of the stopper
just after the release will have a small upward component and a large eastward
component.
|
|
| 12. | For a
constant radius and frequency of revolution of the stopper, the magnitude of the centripetal
acceleration is directly proportional to m.
|
Multiple Choice
Identify the
letter of the choice that best completes the statement or answers the question.
|
|
|
Questions 13 to 18 relate to the situation in Figure 2, in which a child on a
toboggan (a system of total mass m) accelerates down a hill of length L inclined at an
angle q to the horizontal in a
time interval  t. The +x and +y directions are
labelled on the diagram. Assume that friction is negligible unless indicated. t. The +x and +y directions are
labelled on the diagram. Assume that friction is negligible unless indicated.
Figure 2
For questions 13 to 18
|
|
| 13. | The
magnitude of the child’s acceleration down the hill is a. | | b. | | c. | g sin 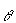 | d. | g cos 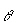 | e. | g tan 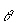 | | |
|
|
| 14. | The
magnitude of the child’s average velocity is
|
|
| 15. | The
magnitude of the force exerted by the toboggan on the hill is a. | mg | b. | mg cos 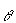 | c. | mg sin
 | d. | mg tan  | e. |  mg sin mg sin  | | |
|
|
| 16. | If the child
starts from rest and accelerates uniformly down the hill, the time required to reach the bottom of
the hill is a. | Lg sin  | b. | 2Lg sin 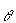 | c. | | d. | | e. | | | |
|
|
| 17. | If  av is the average velocity and av is the average velocity and  is the
instantaneous velocity, then at the halfway point in the journey down the hill is the
instantaneous velocity, then at the halfway point in the journey down the hill
|
|
| 18. | If the
situation in Figure 2 is changed so that there is a coefficient of kinetic friction
mK between
the toboggan and the hill, then the magnitude of the child’s acceleration down the hill
is a. | | b. | g(sin  + mK cos + mK cos  ) ) | c. | | d. | | e. | none of
these | | |
|
|
| 19. | A car of
mass m collides head-on with a truck of mass 5m. If  C®T and C®T and  T®C are the
forces respectively exerted during the collision on the car by the truck and on the truck by the car,
then T®C are the
forces respectively exerted during the collision on the car by the truck and on the truck by the car,
then
|
|
| 20. | A monkey
throws a walnut from a tree, giving the walnut an initial velocity of 2.5 m/s [down]. Air resistance
is negligible. After being released, the walnut experiences an acceleration of a. | 9.8 m/s2
[up] | b. | 9.8 m/s2
[down] | c. | less than 9.8 m/s2 [down] | d. | more than 9.8
m/s2 [down] | e. | zero | | |
|
|
| 21. | A rocket of
mass m is at a distance 3rE from Earth’s centre when its engines are
fired to move it to a distance 6rE from Earth’s centre. Upon reaching its
destination, its new mass is  since fuel is consumed in
the burn. The ratio of Earth’s gravitational force on the rocket at the first location to the
gravitational force on the rocket at the second location is since fuel is consumed in
the burn. The ratio of Earth’s gravitational force on the rocket at the first location to the
gravitational force on the rocket at the second location is a. | 8:1 | b. | 4:1 | c. | 2:1 | d. | 1:4 | e. | 1:8 | | |
|
|
| 22. | Which of the
following is a list of all the forces that act on a satellite in circular orbit around
Earth? a. | the force due to the
satellite’s motion and the force of gravity toward Earth | b. | the force due to the
satellite’s motion, the centrifugal force, and the force of gravity toward
Earth | c. | the centrifugal force and the force of gravity toward
Earth | d. | the centripetal force and the force of gravity toward
Earth | e. | the force of gravity toward Earth | | |
|
|
| 23. | A stunt
airplane flies in a vertical circular loop of radius r at a constant speed. When the airplane
is at the top of the loop, the pilot experiences an apparent weight of zero. The speed of the
airplane is
|
|
| 24. | A 9.5-kg box
is initially stationary on a horizontal table. The coefficient of kinetic friction between the table
and the box is 0.49. The coefficient of static friction is 0.65. The magnitude of the minimum force
needed to set the box into motion is a. | 4.7 N | b. | 6.2 N | c. | 93 N | d. | 61 N | e. | 46 N | | |
|
Completion
Complete each sentence or
statement.
|
|
|
State the number of significant digits in each
measurement or answer of the operation:
|
| | 25. | 0.0501 N
_______
|
| | 26. | 3.00  105 km/s _______ 105 km/s _______
|
| | 27. | 25.989 m +
25.98 m + 25.9 m + 25 m _______
|
| | 28. | 65.98 m  11.5 s 11.5 s  2.0 s _______ 2.0 s _______
|
Matching
|
|
|
Beside each
number, place the letter that matches the best choice. Use the choices listed below. a. | directly proportional
to | b. | inversely proportional
to | c. | proportional to the
square of | d. | inversely proportional to the square of | e. | proportional to the
square root of | f. | inversely proportional to the square root of | g. | independent
of | | |
|
|
| 29. | For an
object moving at a constant velocity, the time interval needed to cover a certain displacement is
_______ the velocity.
|
|
| 30. | When a ball
is undergoing projectile motion, the horizontal motion is _______ the vertical
motion.
|
|
| 31. | For a car
that starts from rest and undergoes constant acceleration, the time interval to cover a certain
displacement is _______ the displacement.
|
|
| 32. | On the
surface of Earth, your weight is _______ the mass of Earth.
|
|
| 33. | For an
object that remains stationary on a horizontal surface, the magnitude of the static friction is
_______ the magnitude of the horizontal force applied to the object.
|
|
| 34. | For
an object undergoing uniform circular motion with a constant radius, the magnitude of the centripetal
acceleration is _______ the speed.
|
|
| 35. | For
an object undergoing uniform circular motion with a constant radius, the force that causes the
centripetal acceleration is _______ the period of revolution of the object.
|
Short Answer
|
|
|
Convert the following measurements:
|
| | 36. | 109 km/h =
_______ m/s
|
| | 37. | 7.16  104 km/min = _______ m/s 104 km/min = _______ m/s
|
| | 38. | 3.4
mm/s2 = _______ m/s2
|
| | 39. | 5.7
cm/(ms)2 = _______ m/s2
|
| | 40. | 4.62  10-3 (km/h)/s = _______ m/s2 10-3 (km/h)/s = _______ m/s2
|
|
|
Beside each
number, place the word, number, phrase, or equation that completes the sentence(s).
|
| | 41. | A windsock
indicates _______ .
|
| | 42. | The three
principal controls a car has for regulating acceleration are _______ , _______ , and _______
.
|
| | 43. | You are
facing southward when suddenly a snowball passes in front of your eyes from left to right. The
snowball was thrown from some distance away with an initial horizontal velocity. The direction of the
instantaneous velocity is now _______ . The direction of the instantaneous acceleration is now
_______ .
|
| | 44. | If the
direction of an object undergoing uniform circular motion is suddenly reversed, the direction of the
centripetal acceleration is _______ .
|
| | 45. | If  LM is 26 m/s [71° W of S], then LM is 26 m/s [71° W of S], then  ML is _______ . ML is _______ .
|
| | 46. | _______ =
 CD + CD +  DE DE
|
| | 47. | The
horizontal acceleration of a projectile is _______ .
|
| | 48. | The
acceleration of an object falling (vertically) through the air at terminal speed is _______
.
|
|
|
Using L, M, and T for the dimensions of length, mass,
and time, respectively, then
|
| | 49. | The
dimensions of the slope of a line on a velocity-time graph are _______
|
| | 50. | The
dimensions of the area under the line on an acceleration-time graph are _______
|
| | 51. | The
dimensions of weight are _______
|
| | 52. | The
dimensions of the universal gravitation constant are _______
|
| | 53. | The
dimensions of gravitational field strength are _______
|
| | 54. | The
dimensions of a coefficient of static friction are _______
|
| | 55. | The
dimensions of frequency are _______
|
| | 56. | The
dimensions of the slope of a line on an acceleration-force graph are _______
|
| | 57. | The law of
inertia is also known as _______ .
|
| | 58. | As the speed
of a flowing river increases, the pressure of the flowing water _______ .
|
| | 59. | An
accelerating frame of reference is also known as _______ . In such a frame, we must invent
_______ to explain an observed acceleration. If the frame is rotating, the invented force is
called _______ .
|
| | 60. | A passenger
of mass m is standing on an elevator that has an acceleration of magnitude a. The
normal force acting on the passenger has a magnitude of _______ if the acceleration is upward, and
_______ if the acceleration is downward.
|
| | 61. | On the
surface of the Moon, your _______ would be the same as on the surface of Earth, but your
_______ would be reduced by a factor of _______ .
|